ÉTUDE D’UNE PERFORMANCE DE LA TROTTINETTE
Contexte : L’utilisation des trottinettes en libre-service se développe exponentiellement. Le taux d’utilisation (nombre d’heure de roulage/jour) a tendance à augmenter. L’autonomie des modèles actuels devient insuffisante, ce qui engendre de nombreux problèmes : frustration des usagers, trottinettes stationnées n’importe où, multiplication des cycles de charge et pertes de productivité…
Problématique : Est-il possible d’accroitre l’autonomie des modèles existants ?
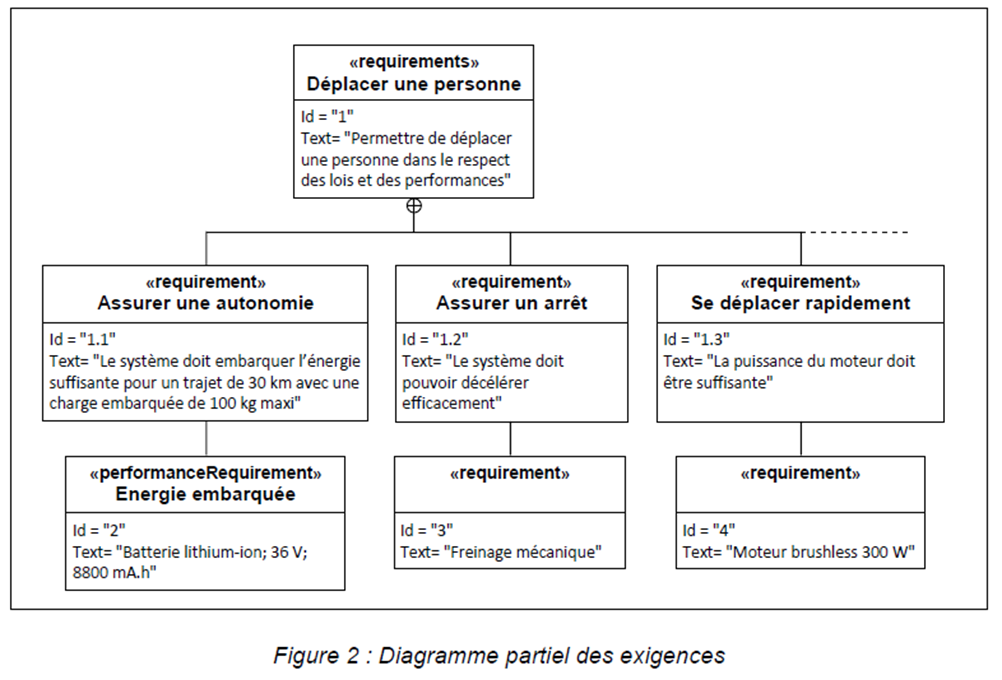
Quelle que soit la valeur trouvée précédemment, on prendra : Ebat = 320 W·h
Le moteur doit fournir une puissance mécanique à la trottinette permettant de vaincre les efforts résistants \(\| \overrightarrow {F_{res}} \|\). Ceux-ci sont estimés à 30 N à 25 km·h-1, sur route horizontale, avec la charge maximale.
Le rendement global de la chaine de puissance vaut \(\eta_g = 78 \%\)
Question I-2
Calculer Pu, la puissance utile de la trottinette, puis Pbat, la puissance fournie par la batterie pour une vitesse de 25 km·h-1
Déterminer le temps tdec pour une décharge complète de la batterie. On considère que la batterie peut être complètement déchargée (ce qui n’est pas le cas en vrai)
Aide : \(W= P \cdot \Delta t\)
En déduire la distance d que l’on peut parcourir avec une batterie complètement chargée (sur le plat, à 25 km·h-1).
Aide : et \(x= \frac{1}{2} \cdot a \cdot t^2 + v_0 \cdot t + x_0\) avec x la distance d. Faire les hypothèses sur l’accélération « a » et la position initiale x0
Deux pistes sont étudiées pour améliorer l’autonomie des trottinettes :
- remplacer les roues par des modèles plus performants afin de diminuer les efforts résistants ;
- changer de batteries pour des modèles avec une capacité plus importante.
1ère piste :
La force résistante s’opposant au roulement des roues est donnée par la formule suivante :
\(F_{Roulement}=\mu_R \cdot \frac{a}{R}\)
avec
R : le rayon de la roue en mm
a : le coefficient de résistance au roulement en mm. On prendra a =3,5 mm
Par ailleurs, les dimensions de la trottinette permettent d’adapter des roues un petit peu plus grandes : 10″ (au lieu de 9″).
Question I-3
Justifier l’intérêt, du point de vue de l’autonomie, d’augmenter la taille des roues.
2ème piste :
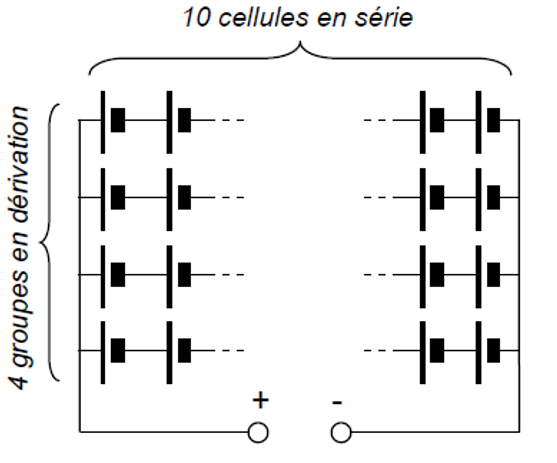
La batterie actuelle est constituée d’un assemblage de cellules lithium-ions de type « 10S4P » : 4 groupes en parallèle de 10 cellules en série (voir figure 3).
Dans un assemblage en série, les tensions sont additionnées. Dans un assemblage en parallèle, la capacité du pack est la somme des capacités de chaque élément (cf. glossaire Batteries, accumulateurs et piles)
Question I-4
Figure 3
Pour une tension nominale de la batterie de 36 V, et une capacité totale de 8,8 A·h, déterminer la tension et la capacité d’une cellule. En déduire la tension et la capacité d’un accumulateur « 10S5P ».
Le fabricant de trottinettes propose de remplacer le pack batterie actuel par un plus performant : tension nominale 36 V, quantité d’énergie stockée 400 W·h. L’encombrement de ce pack batterie est compatible avec les trottinettes.
Un modèle numérique a permis d’obtenir les courbes figure 4, qui donnent, en fonction du temps (en s) la tension électrique (en V) et la distance parcourue (en m) pour la batterie actuelle et la nouvelle batterie :
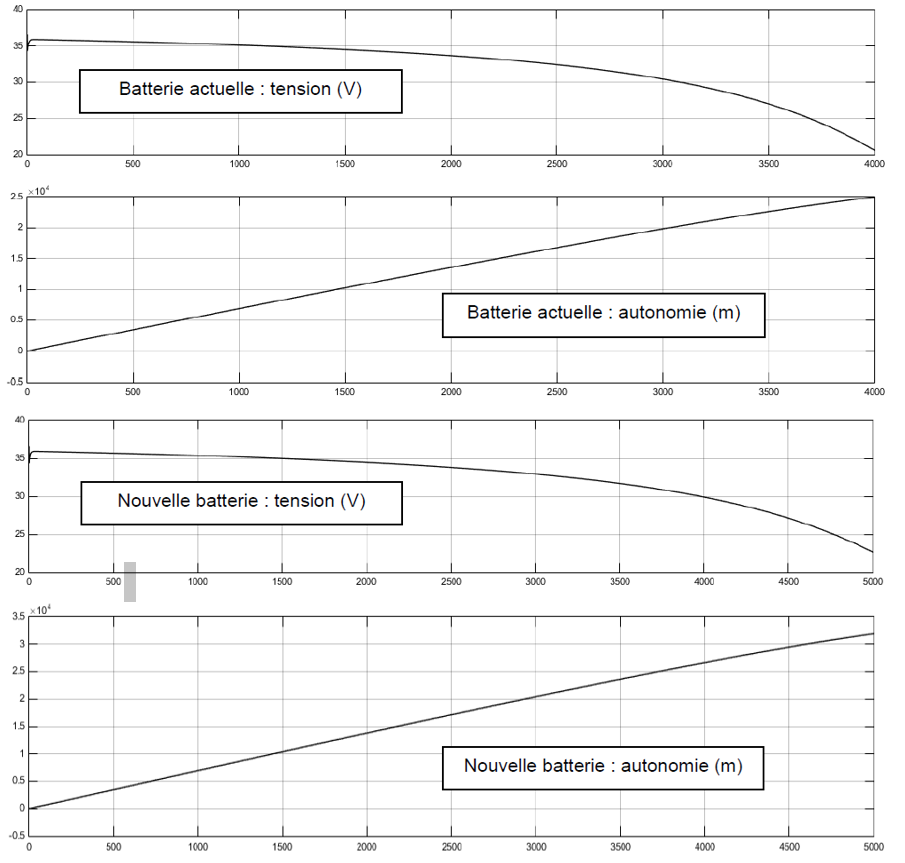
Sachant que pour ce type de batterie, il ne faut pas que la tension descende en dessous de 25 V, sous peine de l’endommager :
Question I-5
Figure 4
Relever l’autonomie simulée (en km) pour les deux batteries. Calculer l’augmentation d’autonomie relative (en %).
