Accès à la présentation de la trottinette.
ÉTUDE D’UNE PERFORMANCE DE LA TROTTINETTE
L’agglomération Lyonnaise (figure 1) a un relief varié. L’Est est relativement plat. Il en est de même pour le secteur de la presqu’île entre Saône et Rhône. Le 4ème arrondissement est constitué essentiellement par le plateau de la Croix Rousse. Le 5ème (colline de Fourvière), le 9ème ainsi que le 1er (pentes de la Croix-Rousse) ont des dénivelés importants, on peut y rencontrer des pentes dépassant les 20%.
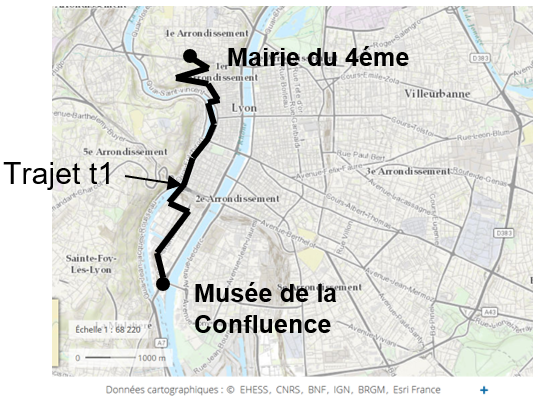
En prenant comme trajet de référence t1, celui qui mène du musée de Confluence à la mairie du 4éme arrondissement (Figure 1), l’opérateur, louant les trottinettes souhaite vérifier à l’aide d’un modèle multi-physique que la trottinette est capable d’effectuer le trajet sans recharge.
Problématique : L’utilisateur de la trottinette, peut-il effectuer un aller/retour sur le trajet t1, avec une batterie pleinement chargée ?
Afin de créer un modèle multi-physique du comportement énergétique de la trottinette, les hypothèses suivantes ont été faites :
– la masse m de l’utilisateur et de sa trottinette est de 83 kg pour une taille de 1m80
– la masse volumique de l’air est égale à 1,2 kg·m-3
– la surface de traînée (S.Cx) est égale à 0,45 m2
– le coefficient de résistance au roulement Crr est égal à 0,015
– accélération gravitation 9.81 m.s-2
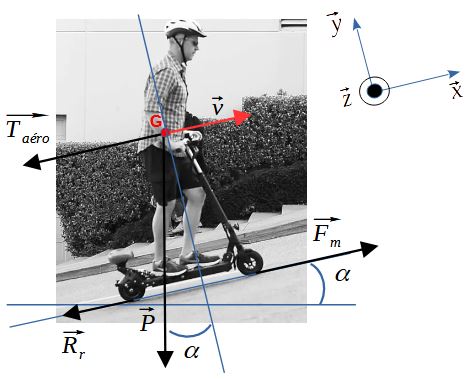
Trois forces s’opposent au déplacement de ’utilisateur et de sa trottinette (figure 3)
Traînée aérodynamique (résistance à la pénétration dans l’air) Taéro :
\(\overrightarrow T _ {aéro}=\frac{1}{2}\cdot \rho \cdot S \cdot C_x \cdot v^2 \cdot \frac {\vec v}{\left\| \vec v \right \|}\)
avec :
Cx : Coefficient aérodynamique
ρ : masse volumique de l’air en kg.m-3
S : surface de référence en m²
v : Vitesse de déplacement en m.s-1
La résistance au roulement Rr est la force résistante due au roulement des pneus sur la chaussée. Elle dépend du coefficient de résistance au roulement Cr et de la masse supportée :
\(R_r=Crr \cdot m \cdot g\)
Le poids P (trottinette + utilisateur) :
\( \overrightarrow P =m \cdot \vec g \)
Un essai dans une pente de 3% avec un utilisateur d’une masse de 70 kg à une vitesse de 5,38 m·s-1, montre que l’intensité de la force de trainée est de 9,2 N, celle de la résistance au roulement des roues au sol est de 12,21 N.
Question I-1
Figure 3
Déterminer la norme de la force motrice \(\vec F_{motrice}\) (\(\vec F_{m}\)) que doit développer la roue motrice avant pour vaincre ces 3 forces résistantes. Calculer la puissance que doit développer le moteur pour ce point de fonctionnement
Aide :
- Écrire tous les vecteurs (force et vitesse) en vecteur colonne (avec les composantes selon x, y et z)
- Appliquer le principe fondamental de la statique \(\sum \vec F_{ext}=\vec 0\)
- Applique le produit scalaire entre le vecteur Force et le vecteur vitesse pour obtenir la puissance.
Question I-2
DR1
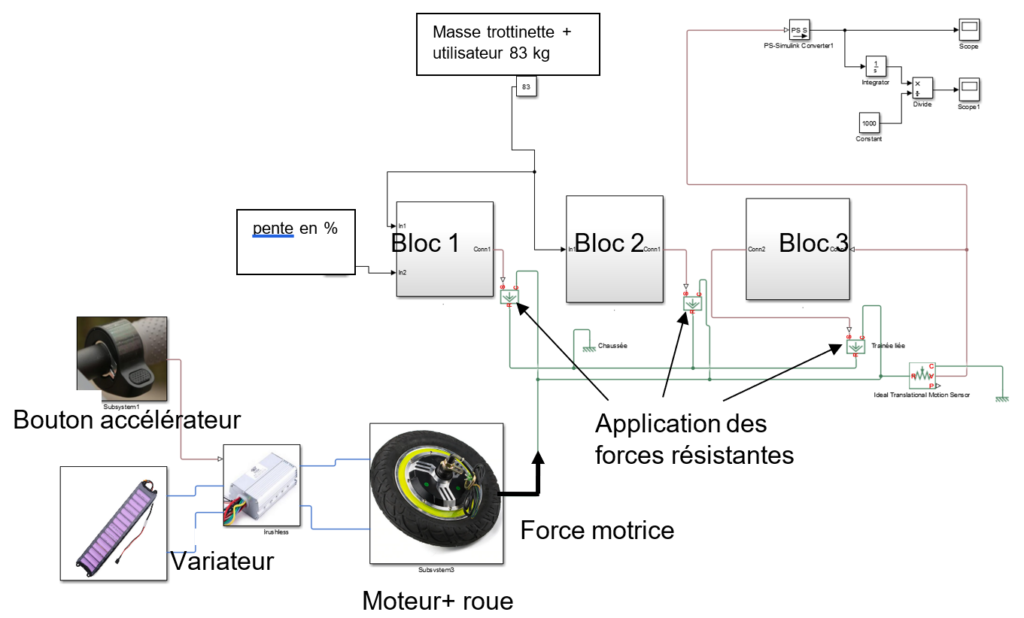
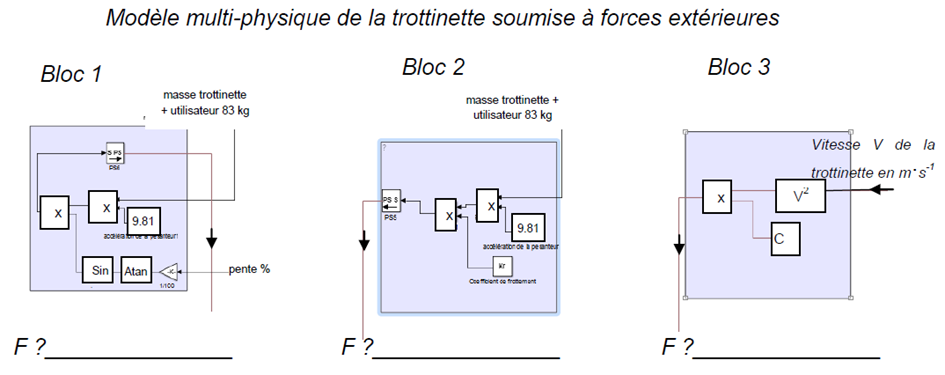
Sur le document réponse DR1, représentant le modèle multi-physique de la trottinette, identifier les blocs modélisant \(\overrightarrow {F_{aéro}}\), \(\vec F_{roulement}\) et \(\vec P\) . Justifier que C = 0,27 dans le bloc 3.
Question I-3
Figure 4
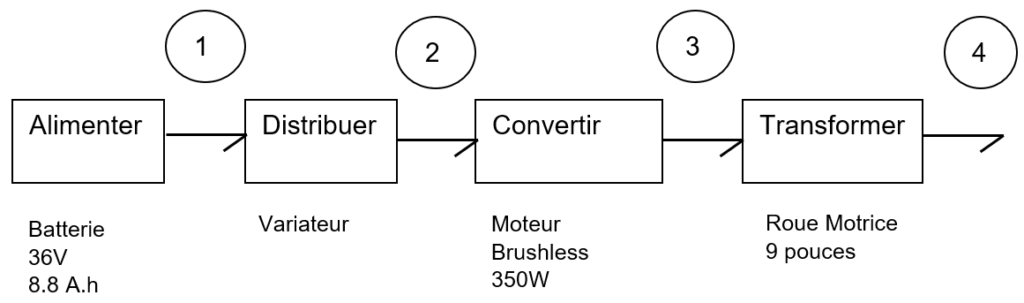
Pour chaque repère (de 2 à 4) de la chaîne de puissance (figure 4), donner le domaine physique de la puissance transmise, et les variables d’effort et de flux associées. Pour cela, recopier et compléter le tableau ci-dessous.

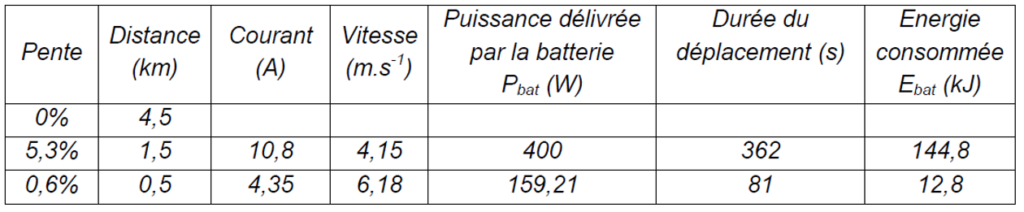
On donne dans le tableau du document réponse DR2 le courant délivré par la batterie et la vitesse de la trottinette fournie par la simulation pour les phases de montée d’une pente à 5,3% et 0,6%. Les temps de trajet ainsi que l’énergie délivrée par la batterie sont calculés.
On admettra que la tension de la batterie Ubat reste égale à 36 V durant l’intégralité du trajet.
Question I-4
Figures 2 et 4
DR2
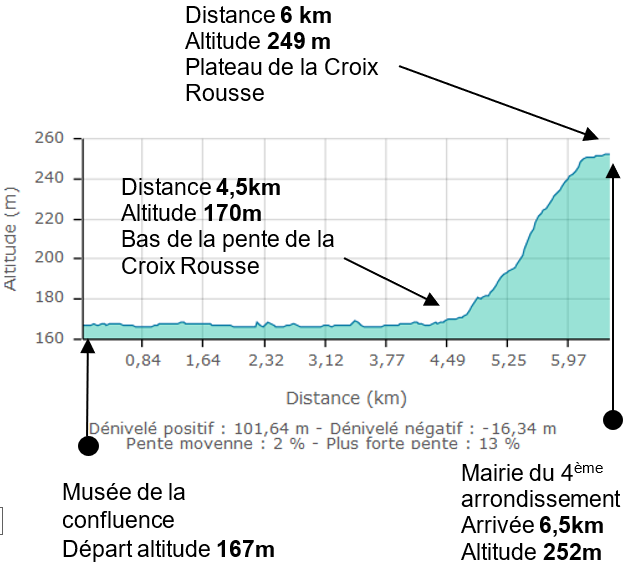
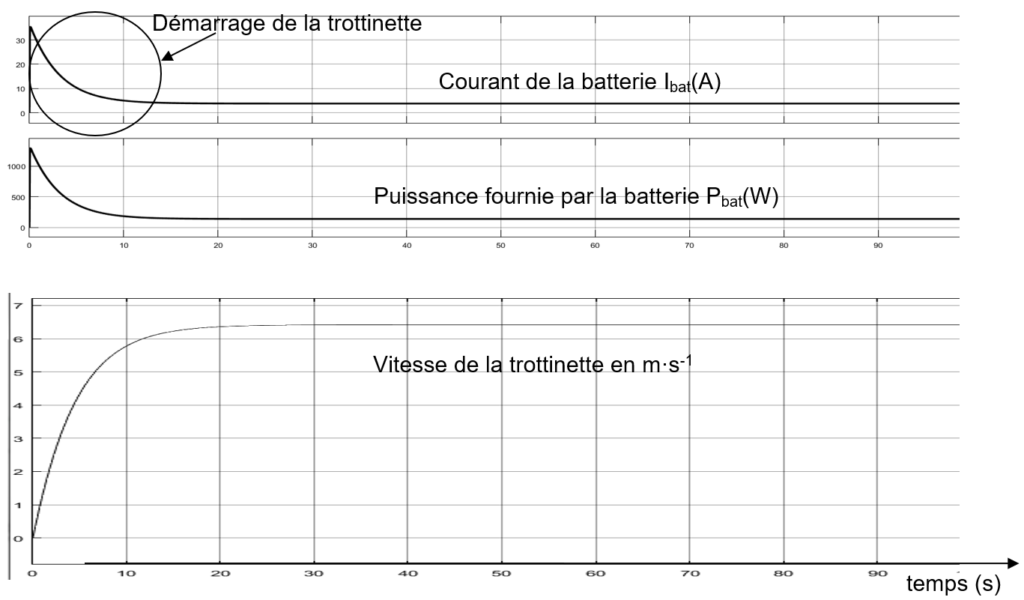
À partir des courbes figure 5, compléter le tableau du document réponse DR2 pour une pente à 0% qui mène du musée de la Confluence au bas des pentes de la Croix Rousse (hors phase de démarrage). Calculer l’énergie totale délivrée au cours du trajet t1 ainsi que la proportion de l’énergie consommée E%Croix_Rousse dans les pentes de la Croix-Rousse par rapport à la consommation totale du trajet Ebat.
La prise en compte, dans le modèle multi-physique, des nombreux démarrages sur ce parcours, fait apparaitre que l’énergie prélevée dans la batterie Etotale est de 480 kJ, dont la moitié dans les pentes de la Croix Rousse.
Question I-5
Énoncer l’hypothèse que l’on peut formuler sur la quantité d’énergie consommée lors de la descente.
Question I-6
Sachant que l’on ne peut utiliser que 80% de l’énergie contenue dans la batterie, conclure sur la problématique : « L’utilisateur de la trottinette, peut-il faire un aller/retour sur le trajet t1, avec une batterie chargée ? ». Calculer l’écart entre l’autonomie réelle de la batterie sur ce type de trajet et celle annoncée par le constructeur.
DOCUMENTS REPONSES
DR1, question I.2
DR2, question I.4