Accès à la présentation de la trottinette.
COMMANDE DU FONCTIONNEMENT DU PRODUIT
Problématique : Peut-on déterminer la présence de la trottinette dans une zone piétonne afin d’adapter sa vitesse maximale autorisée ?
Question II-1
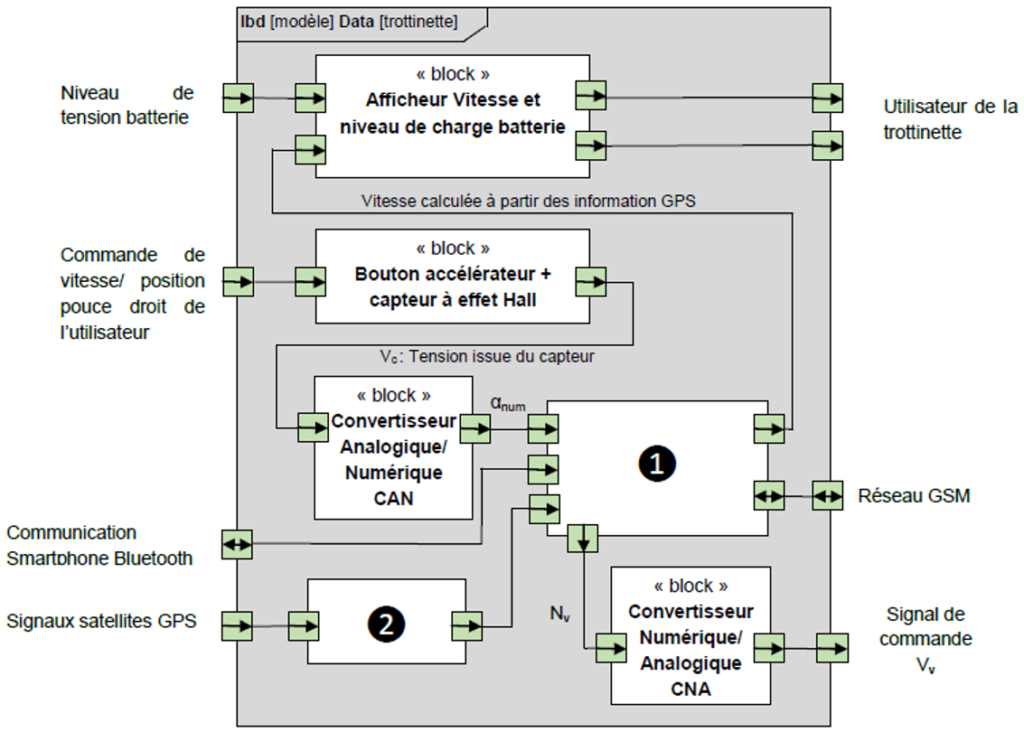
Figure 5
Nommer les blocs ❶ et ❷ du diagramme de blocs internes figure 5.
Le module GPS G70020-KT communique avec le microcontrôleur Qualcomm ARMv7 par l’intermédiaire du protocole UART.
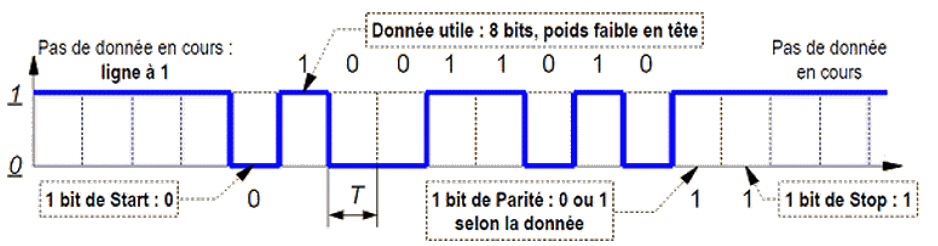
Dans l’exemple de la figure 6, l’octet envoyé est (01011001)2 = (59)16.
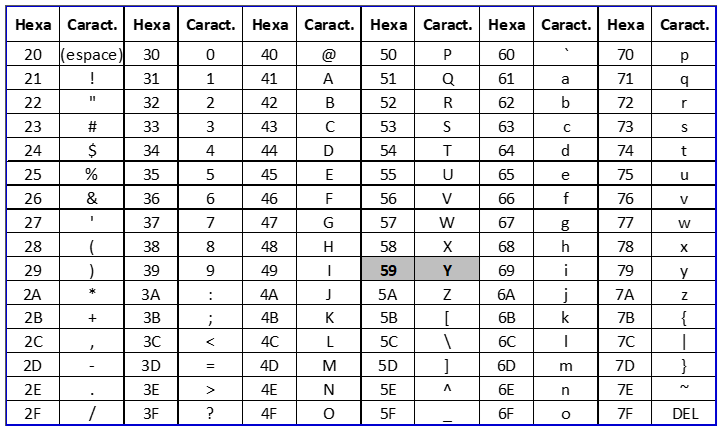
La table ASCII de la figure 7 ci-contre permet de traduire la donnée en caractère : « Y ».
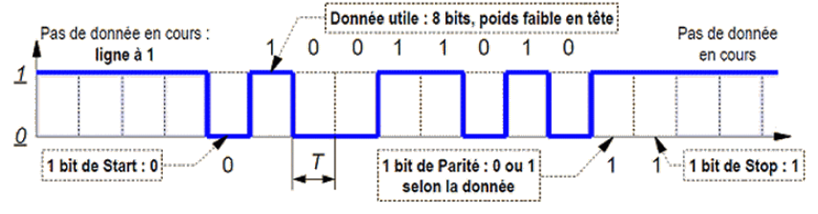
Le relevé du début d’une trame envoyée par le GPS a donné la figure 8 ci-dessous
Question II-2
Figure 8
Indiquer les deux caractères reçus. Calculer le débit d’information en bit·s-1
La norme NMEA est utilisée pour transmettre les coordonnées de la trottinette en caractère ASCII du récepteur GPS jusqu’au microcontrôleur. Il existe plusieurs types de trames. La trame GGA est la plus couramment utilisée par les modules de communication des récepteur GPS. Chaque champ est séparé par une virgule, même s’il est vide. Le tableau figure 9 donne un exemple de trame.
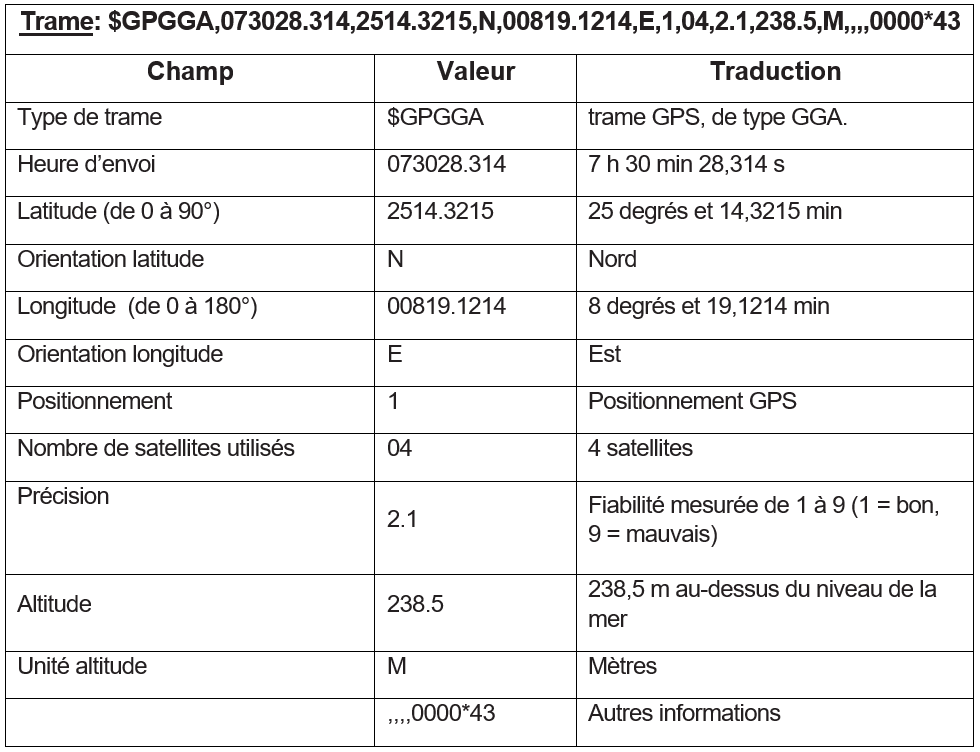
Au départ d’un trajet, la position d’une trottinette est donnée par la trame suivante :
$GNGGA,213405.051,4577.4215,N,00482.7913,E,1,04,2.6,254.0,M,,,,0000*51
Question II-3
Déterminer les coordonnées géographiques (latitude et longitude) de la trottinette. Préciser à quelle heure cette position a été transmise.
Les coordonnées géographiques du centre de Lyon sont :
Latitude : 45 degrés et 44,9076 minutes Nord,
Longitude : 4 degrés et 50,8026 minutes Est.
La circonférence de la Terre mesurée sur un méridien vaut 40007,8 km. Mesurée au niveau du 45ème parallèle, elle vaut 28337,3 km.
Question II-4
Figure 10
Calculer, en mètres, la précision théorique de positionnement obtenue avec les coordonnées précédentes.
Pour déterminer si la trottinette se trouve dans une zone piétonne, délimitée par un polygone, il est possible d’utiliser la méthode « du nombre d’intersections », illustrée sur la figure 11.
On choisit un point O, extérieur au polygone (S1, S2, …, S10). Pour savoir si un point M est à l’intérieur, il suffit de compter le nombre ‘NI’ d’intersections entre le segment [OM] et les côtés du polygone. Si NI est impair, M est à l’intérieur (cas des points M1 et M4). Si NI est pair, M est à l’extérieur (cas des points M2, M3 et M5).
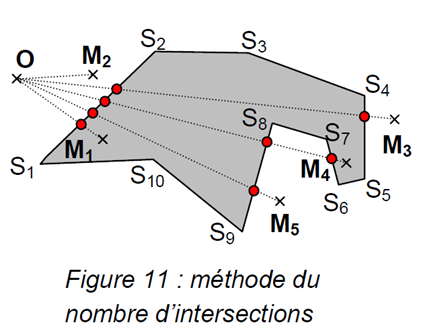
Les cas particuliers où M est sur un côté ou un sommet du polygone ne sont pas étudiés.
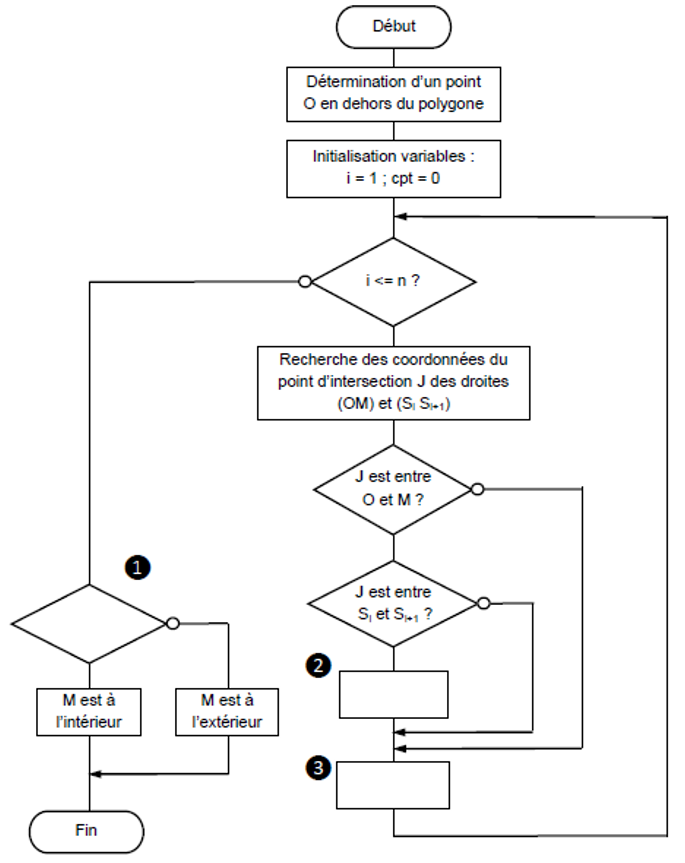
L’algorigramme du document réponse DR1 permet, connaissant les coordonnées des n sommets Si d’un polygone, de déterminer si un point M est à l’intérieur ou pas.
Question II-5
DR1
Compléter les cases ❶, ❷ et ❸ de l’algorithme sur le document réponse DR1
Question II-6
Conclure sur la réponse à la problématique (Comment déterminer la présence de la trottinette dans une zone piétonne afin d’adapter sa vitesse maximale autorisée ?) au regard des différentes questions posées.
DOCUMENT REPONSE
Question II.5