
Optimiser la consommation énergétique du métro rennais
- 1 – Présentation
- 2 – Optimisation des temps séparant les rames successives
- 3 – Rattrapage d’un retard généré par un incident mineur
- 4 – Stockage de l’énergie de freinage par volant d’inertie
- 5 – Optimisation du chauffage des voies
- 6. Synthèse
- DOCUMENTS TECHNIQUES
- DOCUMENTS REPONSES
Présentation
Le métro de Rennes (de type VAL : Véhicule Automatique Léger) est un système de transport en commun entièrement automatique, développé par la société Siemens France.
Sans conducteur, il ne nécessite aucun personnel d’exploitation à bord des véhicules ainsi qu’en station.
Inauguré le 15 mars 2002, le métro rennais ne comporte qu’une seule ligne représentée sur la figure 1.
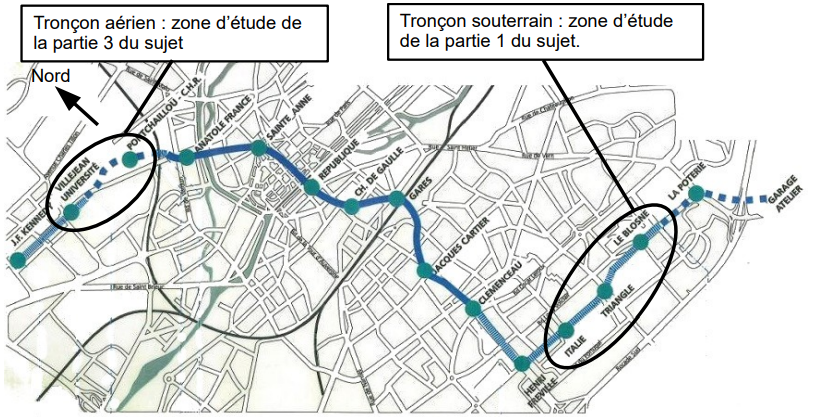
Ce métro, alimenté en énergie électrique et équipé de pneus, figure parmi les modes de transport les plus silencieux et les plus propres.
Le pilotage centralisé et distant permet à chaque instant d’adapter le nombre de rames à l’affluence des voyageurs.
La société Kéolis, en charge de l’exploitation du métro, fait en sorte de minimiser sa consommation d’énergie en mettant en œuvre des solutions innovantes autour desquelles s’articule le questionnement proposé.
Les deux postes importants de consommation d’énergie sont l’alimentation des rames (une rame est constituée de deux voitures, voir figure 2) et le chauffage des voies (bandes de roulement des pneus).
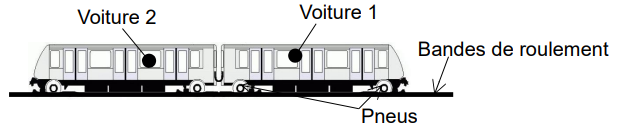
En conséquence, les pistes privilégiées pour réduire l’énergie consommée par la société Kéolis sont étudiées dans les parties suivantes :
- optimisation des temps séparant les rames successives (partie 2) ;
- rattrapage du retard généré par un incident mineur (partie 3) ;
- stockage de l’énergie de freinage par volant d’inertie (partie 4) ;
- optimisation du chauffage des voies (partie 5).
Toutes les parties sont indépendantes
2 – Optimisation des temps séparant les rames successives
Objectif(s) de cette partie : vérifier qu’un choix judicieux des temps séparant les rames est une solution à la réduction de la consommation énergétique du métro.
La réversibilité énergétique des rames autorise des transferts d’énergie électrique des rames en décélération vers celles en demande d’énergie.
Dans le cas où aucune rame n’est en demande d’énergie, l’énergie de freinage est dissipée sous forme de chaleur dans un banc rhéostatique et est donc perdue.
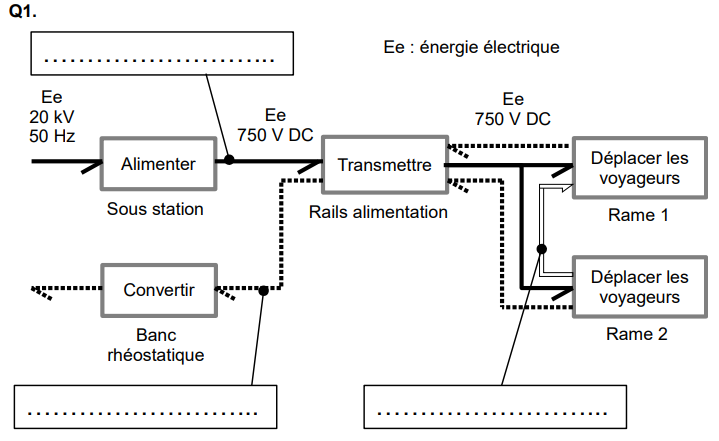
Le document réponse DR1 page 25 illustre les transferts d’énergie, depuis le réseau électrique d’alimentation jusqu’aux rames (seules deux rames sont représentées). Lors de l’accélération des rames et en l’absence de rame en décélération, le transfert d’énergie est qualifié « transfert normal ».
Lorsqu’une ou plusieurs rames sont en décélération, l’énergie cinétique de décélération est transformée en énergie électrique. Deux cas peuvent se produire :
- aucune rame n’est en phase d’accélération, le transfert d’énergie est qualifié « transfert rhéostatique »
- une ou plusieurs rames sont en phase d’accélération, le transfert d’énergie est qualifié « transfert revalorisé »
Q1. Sur le document réponse DR1, indiquer dans les cadres les types de transfert d’énergie (normal, rhéostatique, revalorisé) en vous basant sur les définitions précédentes.
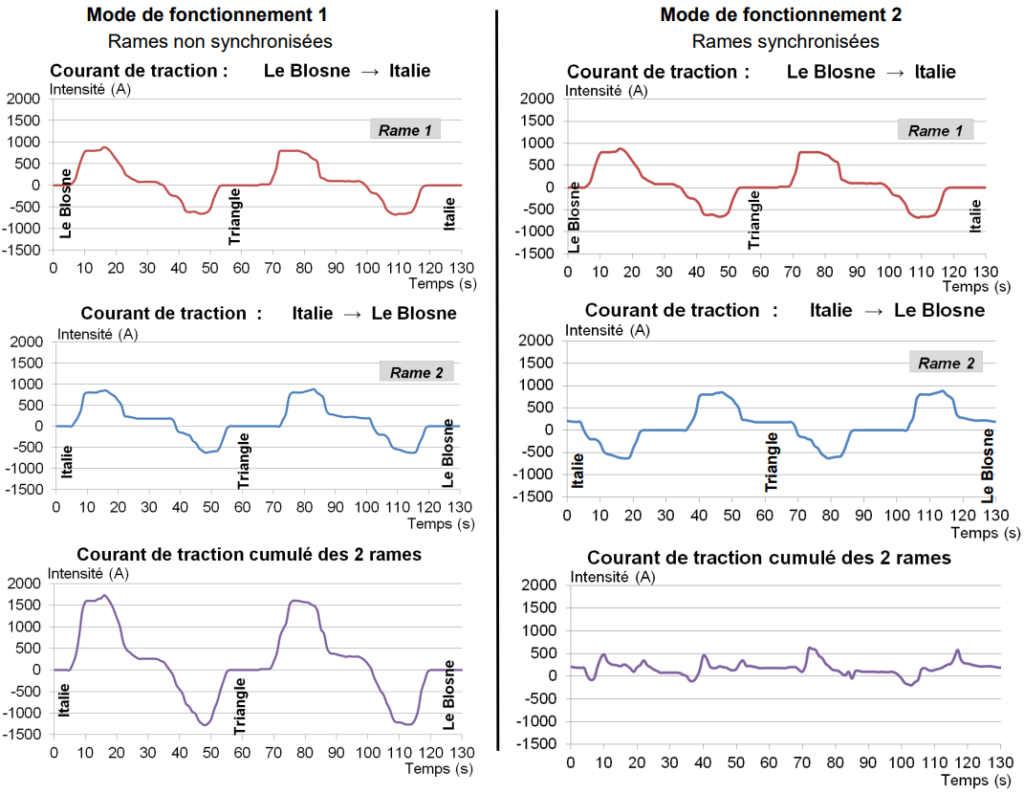
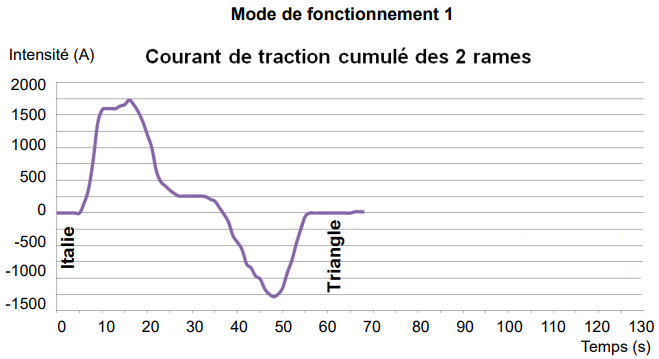
Afin d’estimer les courants absorbés et restitués par les rames (courant de traction) lors de leur déplacement, la société Kéolis a procédé à des relevés d’intensité de courant pour deux modes de fonctionnement distincts, avec deux rames en circulation en sens opposés, entre les stations Le Blosne et Italie (voir figure 1 et document technique DT1).
Dans le mode de fonctionnement 1, l’essai a été réalisé sans synchronisation des accélérations et freinages des deux rames en sens opposés.
Dans le mode de fonctionnement 2, l’essai a été réalisé avec synchronisation des accélérations et freinages des deux rames en sens opposés.
Q2. À l’aide du document technique DT1, pour le mode de fonctionnement 1, indiquer si la rame 1 consomme de l’énergie ou si elle en restitue pour les intervalles de temps [5 s ; 35 s] et [35 s ; 52 s].
La tension d’alimentation des rames est de 750 V continue supposée constante.
Q3. À partir du document réponse DR2 (issu du document technique DT1), estimer de manière approchée, l’énergie fournie par le réseau (en W∙h) aux 2 rames entre les stations Italie et Triangle lors du mode de fonctionnement 1. Faire apparaître sur le document DR2 les tracés qui permettent de réaliser cette estimation.
Q4. À l’aide du document technique DT1, expliquer pourquoi le courant de traction cumulé obtenu lors du mode de fonctionnement 2 est l’amplitude plus faible que celui obtenu lors du mode de fonctionnement 1.
L’énergie consommée par les deux rames lors du mode de fonctionnement 2 a été estimée à 2 800 W∙h entre les stations Le Blosne et Italie.
Q5. Déterminer le pourcentage d’énergie non consommée dans le mode de fonctionnement 2 par rapport au mode de fonctionnement 1.
Dans un souci d’optimisation énergétique, la société Kéolis cherche à se rapprocher du mode de fonctionnement 2. Cependant, le nombre de rames en circulation sur une journée fluctue de 6 à 22 en fonction de l’affluence des voyageurs.
La figure 3, issue de relevés expérimentaux, montre la corrélation qui existe entre le nombre de rames en circulation, les temps séparant deux rames successives et le pourcentage d’énergie non revalorisée (énergie perdue). Elle met en évidence la nécessité d’éviter certains temps séparant les rames (exemple : cinq rames en circulation avec un temps les séparant de 435 s).
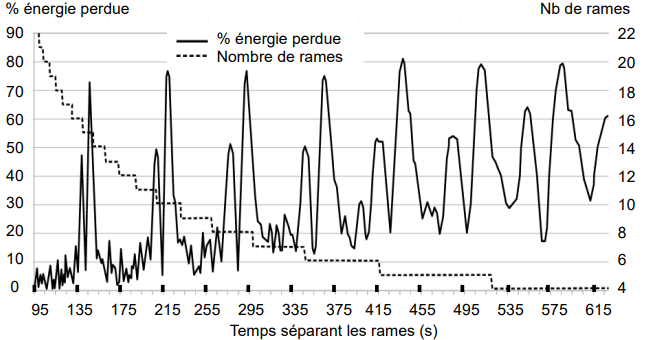
rames en circulation.
Q6. Indiquer la plage de temps permettant un fonctionnement à sept rames avec une énergie de freinage perdue inférieure à 30 %.
Lors d’une augmentation de l’affluence des usagers, le pilotage centralisé du métro décide de passer de sept rames à neuf rames en circulation. Les rames sont insérées une à une sur la ligne de métro jusqu’à obtention du nombre souhaité.
Q7. À l’aide de la figure 3, expliquer pourquoi ce mode d’insertion des rames sur la ligne a une incidence sur l’énergie perdue. Critiquer la valeur obtenue à la question Q5 pour le pourcentage d’énergie non consommée.
3 – Rattrapage d’un retard généré par un incident mineur
Objectif(s) de cette partie : proposer une solution pour rattraper le retard engendré par un incident mineur afin de respecter l’intervalle prévu.
Les études menées dans la partie 2 ont permis de montrer l’intérêt de cadencer judicieusement les différentes rames du métro afin de réduire sa consommation énergétique. Cependant, des incidents mineurs (porte bloquée…) perturbent quotidiennement le respect des intervalles.
Ces aléas sont connus et ne provoquent généralement que des retards modérés allant de 1 à 22 secondes qui doivent être rattrapés sur un nombre limité de trajets d’inter-stations.
Lois de vitesses suivies par les rames
La figure 4 représente la loi de vitesse d’une rame en fonction du temps V=f (t) entre les stations Ponchaillou et Villejean Université (voir figure 1) dans les conditions normales de fonctionnement appelées mode « non dégradé ».
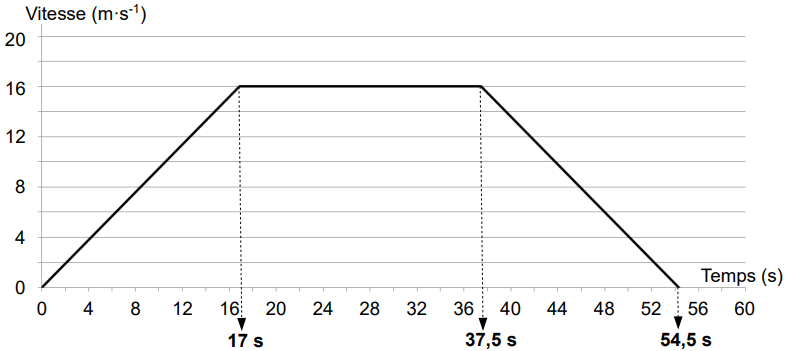
(V =f (t ))
Q8. À partir de la loi de vitesse V=f (t) (figure 4), calculer la distance x parcourue entre les instants 0 s (départ station Ponchaillou) et 54,5 s (arrivée
station Villejean Université).
La vitesse des rames est en fait gérée par la loi V=f (x) représentée sur la figure 5 (vitesse V en fonction de la position x) qui a été obtenue à partir de la loi V=f (t) (figure 4).
En cas d’incidents mineurs, le mode « dégradé » doit permettre à une rame de rattraper son retard sur quelques inter-stations. La figure 5 montre qu’en mode « dégradé », la phase de déplacement à vitesse constante n’existe plus.
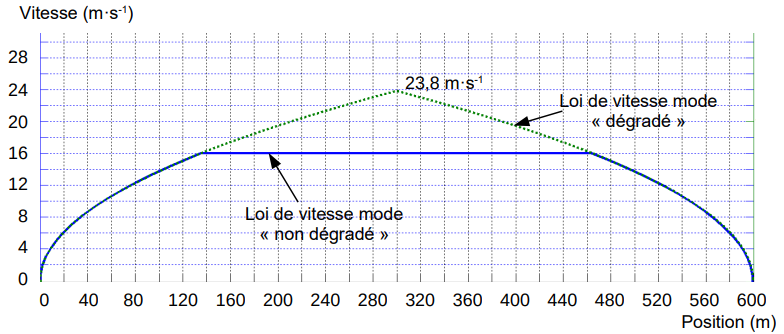
Les valeurs des accélérations et décélérations de la rame sont identiques, en mode « non dégradé » et « dégradé » et considérées constantes.
Pour le mode « dégradé » la vitesse atteinte en fin de phase d’accélération est de 23,8 m⋅s−1 (voir figure 5).
Q9. Déterminer le temps tdeg mis par la rame pour effectuer le déplacement de 600 m (distance séparant les deux stations) en mode « dégradé ».
Q10. Conclure sur le gain de temps réalisable et sur le nombre d’inter-stations à parcourir pour récupérer un retard de 22 secondes en faisant l’hypothèse simplificatrice que les stations sont équidistantes et que les profils de vitesse sont identiques entre stations.
Incidence du profil de la voie de circulation des rames
L’étude précédente a permis de montrer que la loi de vitesse en mode « dégradé » entre les stations Ponchaillou et Villejean Université permet de rattraper une partie du retard.
Cependant, cette interstation présente deux particularités nécessitant de vérifier que la rame est capable de suivre la loi de vitesse en mode « dégradé ». En effet, cette interstation est une portion aérienne, soumise aux intempéries et présentant le plus fort dénivelé de la ligne du métro (pente de 8 % équivalant à un angle θ de 4,6° représenté sur la figure 6).
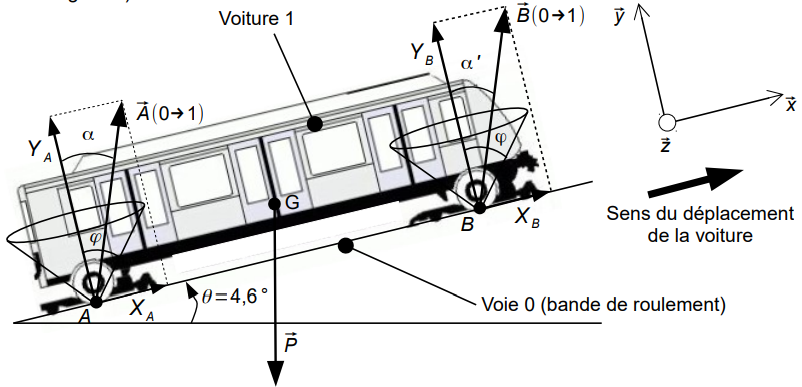
Remarque : l’inclinaison de la voie n’est pas représentée à l’échelle et aucune mesure n’est à prendre sur la figure 6.
L’étude sera menée dans le plan de symétrie (O , ⃗x ,y⃗) .
Les données sont les suivantes :
- masse d’une voiture, mV=14000 kg
- nombre maximal de passagers par voiture, 75, soit une masse mP=7500 kg ;
- accélération limitée à aG=1,3 m⋅s−2
- pour le confort des passagers
- action de l’air sur la voiture et résistance au roulement négligées au regard des autres actions en présence
- accélération de la pesanteur, g≈9,81 m⋅s−2
Les actions mécaniques extérieures appliquées à la voiture (1) sont :
- \(\vec P\), le poids de la voiture et des usagers appliqué en G ;
- \(\overrightarrow{A_{(0→1)}}\) l’action de la voie sur la voiture appliquée en A.
- \(\overrightarrow{B_{(0→1)}}\) action de la voie sur la voiture appliquée en B.
- L’étude sera menée sur une seule voiture dans la position de la figure 6 en phase d’accélération.
Q11. Lors de la phase d’accélération, déterminer sous forme littérale, l’équation de la résultante dynamique projetée sur ⃗x appliquée à la voiture (1) isolée. En déduire l’expression de XA+ XB en fonction de aG , mV , mP , θ , et g.
Les couples délivrés par les roues motrices avant et arrière étant considérés équivalents, les efforts tangentiels X A et XB sont par conséquent égaux.
Q12. Déterminer l’expression littérale de X A puis effectuer l’application numérique.
Les équations des moments dynamiques aux points A et B ont permis de déterminer les efforts normaux aux contacts de la voie (0) sur la voiture (1).
Les résultats sont les suivants : YA=110 kN et YB=100 kN.
Le coefficient de frottement entre le rail (acier grenaillé) et les pneus est égal à f =tan φ=0,3 lorsque la voie est humide.
Q13. Écrire la condition de non glissement des roues aux points A et B, effectuer l’application numérique et conclure sur la capacité de la voiture à accélérer sur la pente à 8 %.
4 – Stockage de l’énergie de freinage par volant d’inertie
Objectif(s) de cette partie : vérifier que le système à stockage inertiel permet la revalorisation des énergies de freinage excédentaires.
Les études précédentes ont montré qu’une bonne gestion des intervalles de temps entre les rames et des retards permet de diminuer l’énergie dissipée dans les bancs rhéostatiques.
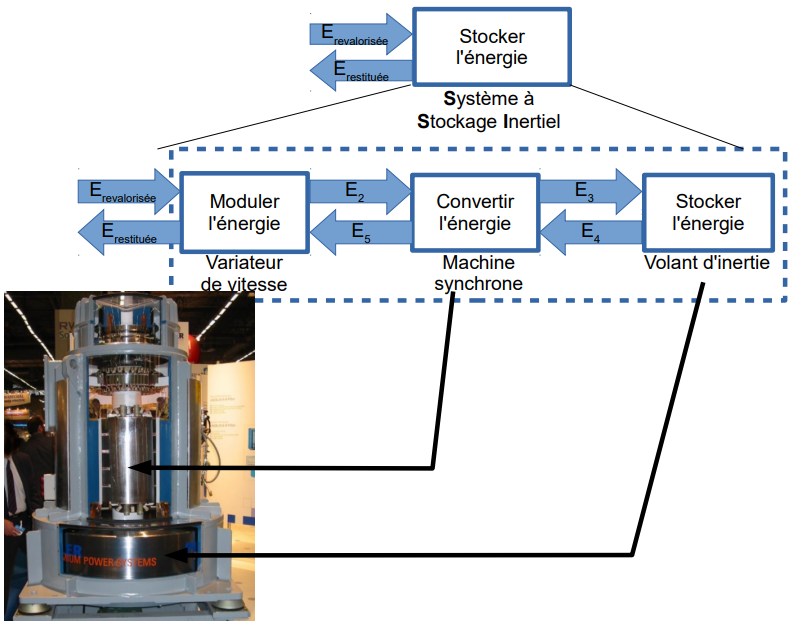
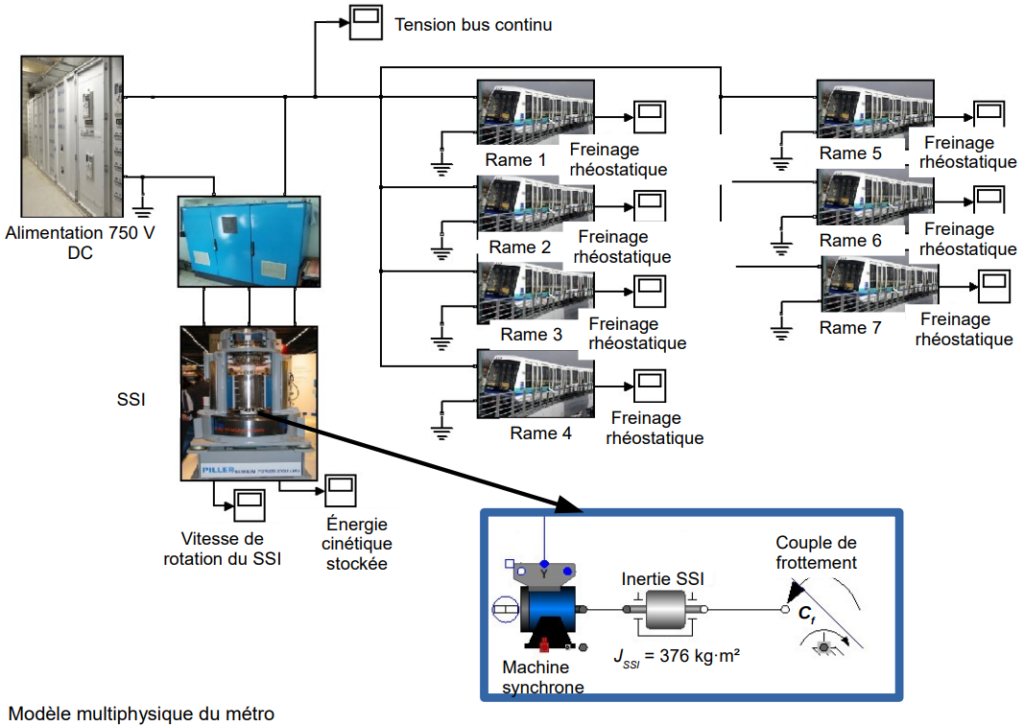
Un système à stockage inertiel (SSI) représenté sur la figure 7, a été mis en place pour limiter ces pertes. Une partie de cette énergie, appelée énergie revalorisée, est stockée dans le volant d’inertie, par l’intermédiaire d’un ensemble machine synchrone-variateur, au lieu d’être dissipée. Elle peut ensuite être restituée aux rames.
Ses caractéristiques sont les suivantes :
- moment d’inertie, JSSI=376 kg⋅m2
- vitesse comprise entre 188 rad·s-1 et 377 rad·s-1
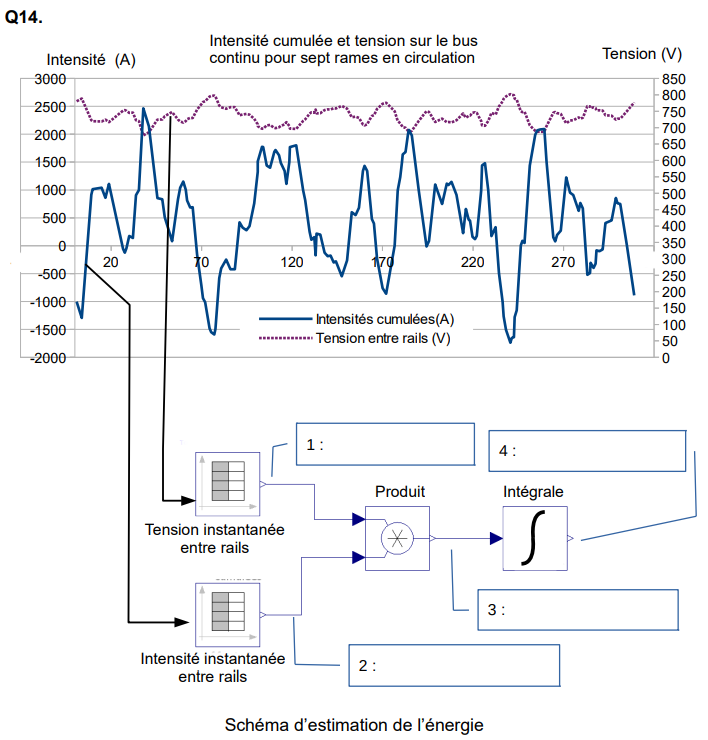
Le schéma du document réponse DR3 page 26, construit à partir des données réelles de l’intensité cumulée pour sept rames en circulation et de la tension entre les rails d’alimentation, indique la méthode qui a permis d’estimer les énergies mises en jeu.
Les transferts d’énergie sont caractérisés par le produit de deux grandeurs « effort » et « flux ».
Q14. Placer sur le document réponse DR3, les informations « grandeur effort », « grandeur flux », «énergie » et « puissance instantanée », dans les cadres repérés de 1 à 4.
À partir de ces données, les énergies consommées avec revalorisation (réutilisation de l’énergie récupérée au freinage) et sans revalorisation (dissipation rhéostatique de l’énergie récupérée au freinage) ont été estimées. Les résultats sont représentés sur la figure 8.
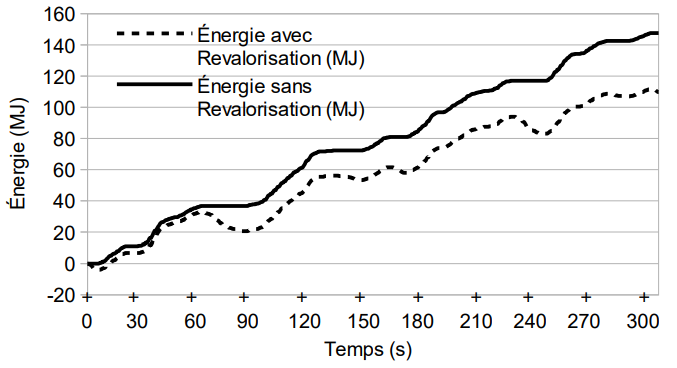
L’énergie récupérable par le SSI est la différence entre l’énergie avec revalorisation et l’énergie sans revalorisation.
Q15. À partir de la figure 8, estimer l’énergie électrique revalorisée Erevalorisée à l’instant t=300 s .
Le rendement, supposé constant, de l’ensemble machine synchrone-variateur ηmv est de 0,84 lors du stockage et de la restitution.
Q16. En déduire l’énergie Erestituée restituée par le SSI.
Afin d’optimiser les performances énergétiques du métro, un modèle multi-physique a été élaboré (voir document technique DT2). Ce modèle a permis d’évaluer l’énergie restituée cumulée par le système à stockage inertiel (SSI) pour sept rames en circulation. La figure 9 met en corrélation les résultats de simulation du modèle avec les résultats expérimentaux.
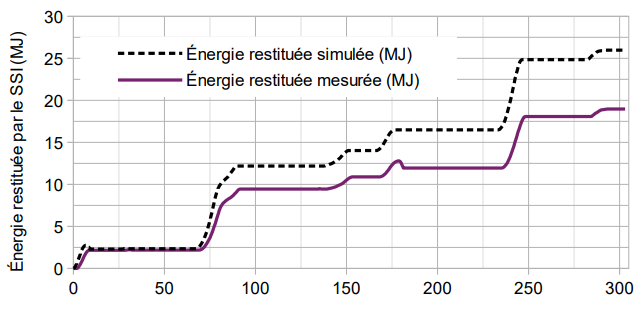
Le modèle sera acceptable dès lors que les écarts relatifs sur les énergies restituées obtenues par le modèle et par les mesures ne divergent pas de plus de 7 % (prendre l’énergie mesurée comme référence) .
Q17. Déterminer en pourcentage, l’écart relatif maximal d’énergie stockée à partir des résultats de la figure 9. Conclure sur la validité du modèle multi-physique.
Afin d’améliorer le modèle multi-physique, une analyse de la vitesse de rotation du SSI est réalisée à partir des données expérimentales et simulées. Les résultats sont donnés figure 10.
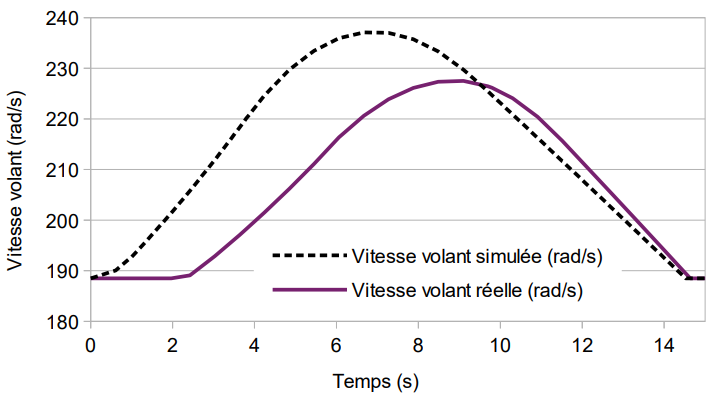
La figure 10 met en évidence les écarts suivants :
- un décalage temporel (négligé dans le questionnement)
- une accélération simulée plus importante
- une décélération simulée plus faible
- un stockage simulé plus important
Q18. À l’aide du document technique DT2 page 21, définir le paramètre du modèle multi-physique à modifier ( JSSI ou Cf ) pour se rapprocher de la réponse réelle. Préciser et justifier s’il faut diminuer ou augmenter ce paramètre.
Le paramètre du modèle modifié précédemment a permis de valider le modèle multiphysique pour sept rames en circulation.
Le réinvestissement de ce modèle pour huit rames en circulation a permis d’estimer l’énergie stockée par le volant d’inertie (figure 11).
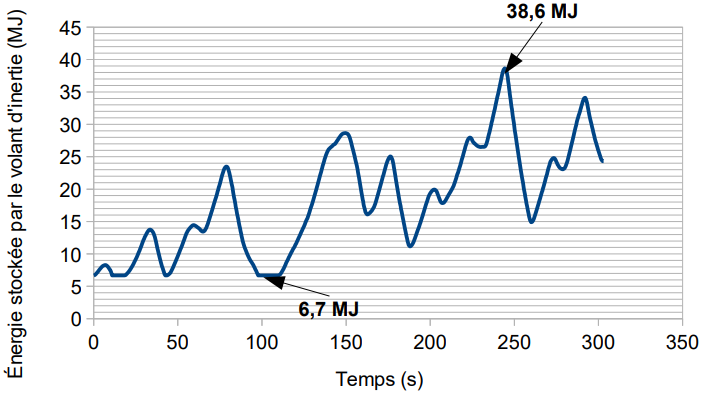
Q19. Calculer la variation d’énergie maximale stockée par le volant d’inertie pour huit rames en circulation. À l’aide de la valeur du moment d’inertie JSSI renseignée dans le modèle multi-physique (document technique DT2), déterminer la vitesse de rotation maximale du volant d’inertie pour huit rames en circulation.
La machine synchrone du SSI étant capable de dépasser une vitesse de 377 rad·s-1, il faut vérifier que le volant d’inertie supporte aussi cette vitesse.
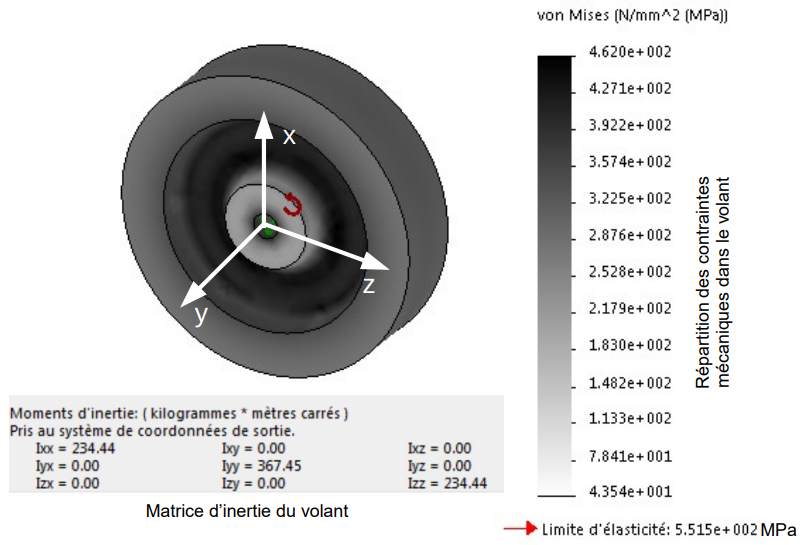
Le modèle volumique du volant (document technique DT3 page 22) a permis d’obtenir la contrainte mécanique équivalente de Von Mises lors d’une mise en rotation à la vitesse maximale précédemment trouvée.
Un coefficient de sécurité CS supérieur ou égal à 2 doit être assuré d’un point de vue de la résistance des matériaux.
Q20. À partir du document technique DT3, indiquer la contrainte équivalente de Von Mises maximale σmaxi atteinte dans le volant et déterminer le coefficient de sécurité CS.
Q21. Conclure sur la capacité du volant à supporter cette survitesse. Indiquer les conséquences sur les transferts énergétiques.
5 – Optimisation du chauffage des voies
Objectif(s) de cette partie : valider la solution technique choisie pour optimiser le chauffage des voies afin de réduire la consommation d’énergie.
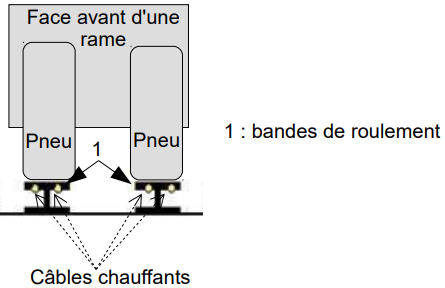
Afin d’éviter l’accumulation de neige ou de glace sur les voies situées en extérieur, plusieurs câbles chauffants alimentés en 750 V continu, sont installés sous les bandes de roulements (voir figure 12). La société Kéolis souhaite améliorer le contrôle du chauffage afin de réduire sa consommation énergétique.
Conditions de mise en chauffe des bandes de roulement
Une station météorologique (voir figure 13), composée notamment d’une sonde de température et d’un capteur d’hygrométrie, mesure les conditions climatiques extérieures qui sont transmises à un automate programmable gérant le chauffage des voies.
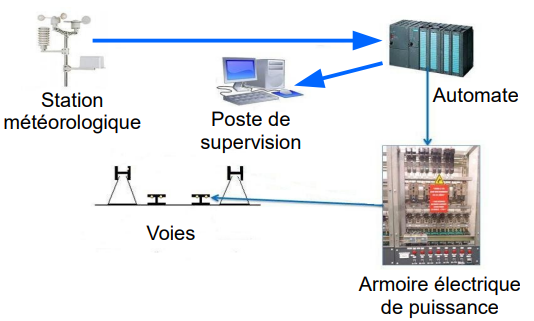
Le chauffage des voies est mis en action lorsque la température extérieure Te devient inférieure ou égale à 4 °C et que le taux d’hygrométrie Hr est supérieur ou égal à 80 %.
Le capteur de température fournit une tension variable entre 0 V et 10 V pour une température évoluant entre -10 °C et 30 °C (soit une pleine échelle de 40 °C). Cette information est numérisée par un convertisseur analogique-numérique 8 bits (CAN).
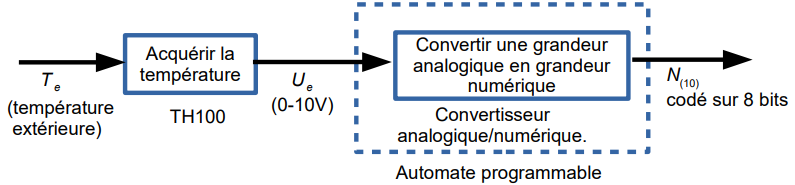
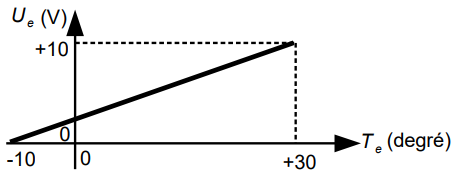
La loi entrée-sortie du capteur de température est de la forme Ue=a⋅Te+b .
Q22. Déterminer la tension Ue pour une température Te=4 ° C .
Q23. Calculer la résolution analogique q (ou quantum) du convertisseur analogique-numérique, sachant que sa plage d’entrée est 0-10 V, et spécifier son unité. Déterminer la valeur décimale N4°C(10) représentant la valeur en sortie du CAN lorsque la température extérieure est de 4 °C.
L’autorisation de fonctionnement du chauffage fonctionne selon le schéma de la figure 16 :
- lorsque la température extérieure Te est inférieure ou égale à 4 °C, le chauffage des voies est activé et restera activé tant que la température extérieure Te sera inférieure à 6 °C
- lorsque que la température extérieure Te est supérieure ou égale à 6 °C, le chauffage est désactivé et restera désactivé tant que la température extérieure Te sera supérieure à 4 °C
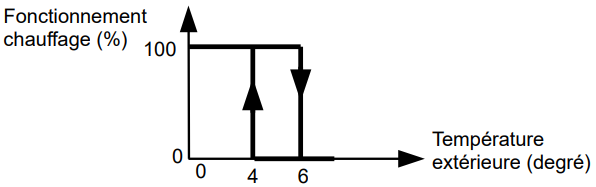
Le fonctionnement est géré par un algorithme utilisant les variables définies ci-dessous :
Hr : hygrométrie.
Te : température extérieure.
Ch : variable de mise à l’arrêt ou en marche du chauffage
Ch = 0 : arrêt.
Ch = 1 : marche.
Q24. Compléter l’algorithme du document réponse DR4
Gestion de la commande de chauffage
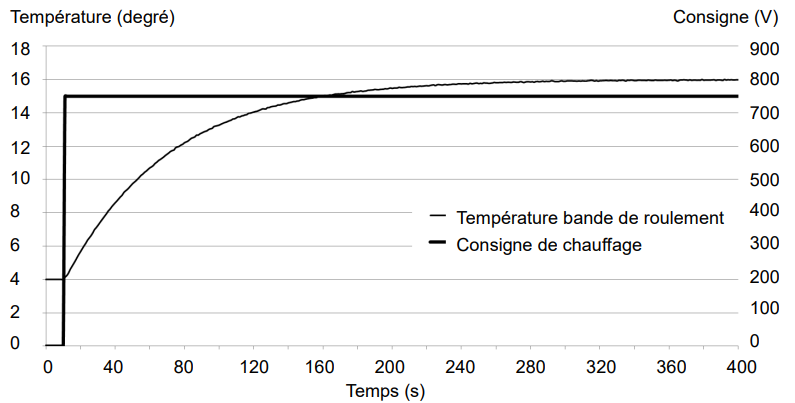
L’étude suivante vise à définir les paramètres de mise en chauffe des bandes de roulement afin de stabiliser leur élévation de température à +8 °C ± 1 °C. Aucun capteur n’étant utilisé pour réguler le système de chauffage, un relevé expérimental du comportement d’une bande de roulement mise en chauffe a été réalisé (figure 17). Ces mesures doivent permettre de modéliser son comportement thermique et ainsi de déterminer les paramètres optimaux de la commande de chauffage.
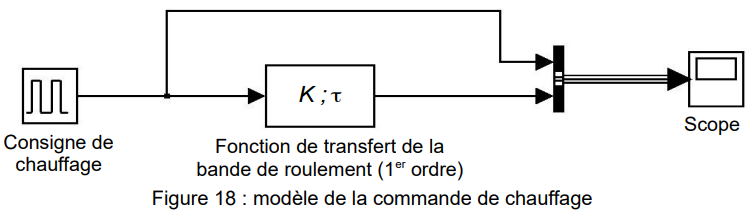
Le modèle de la commande de chauffage est représenté sur la figure 18
Q25. À l’aide du relevé expérimental figure 17 et du document technique DT4, déterminer l’amplification statique K et la constante de temps τ en vue de paramétrer le modèle de comportement de la bande de roulement. Préciser les unités.
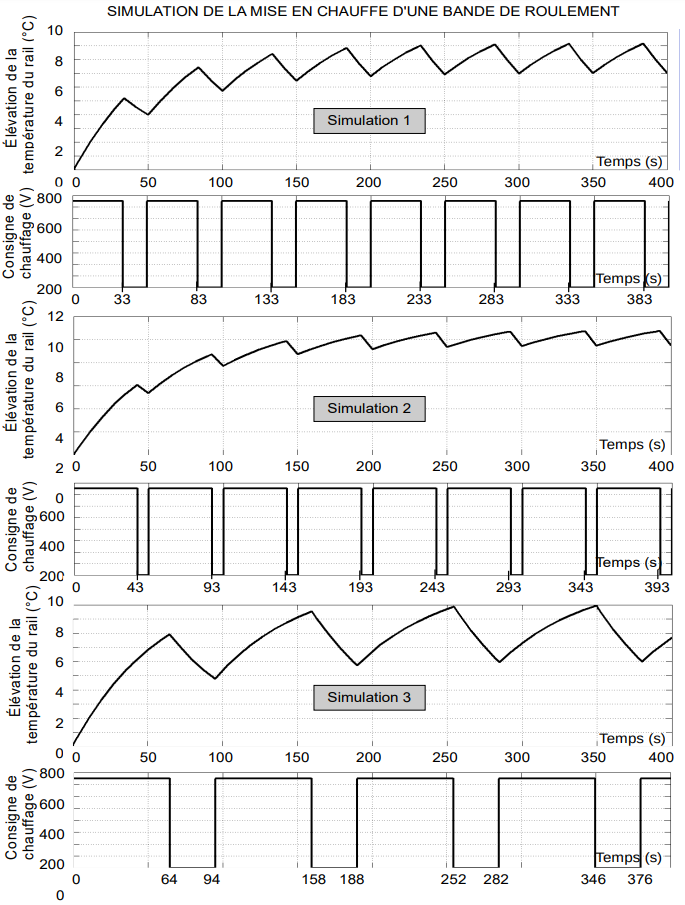
Le document technique DT5 page 24 montre trois simulations de mise en chauffe d’une bande de roulement.
Q26. En justifiant la réponse, préciser quelle simulation correspond à l’élévation de température attendue (+8 °C ± 1 °C). Pour la simulation retenue, déterminer la période T et le rapport cyclique α à paramétrer dans le bloc commande de chauffage. Estimer en pourcentage, le gain énergétique réalisable par rapport au fonctionnement actuel ( α=1 ).
6. Synthèse
Objectif(s) de cette partie : proposer et justifier les choix énergétiques de la future ligne de métro de l’agglomération rennaise
Une seconde ligne de métro sans conducteur est actuellement en construction dans l’agglomération rennaise. Sa mise en service est prévue pour l’année 2020.
Q27. En s’appuyant sur les études précédemment menées, proposer et justifier les choix à mettre en place pour minimiser la consommation énergétique de la future ligne de métro (dix lignes maximum).
DOCUMENTS TECHNIQUES
Document technique DT1
Document technique DT2
Document technique DT3
Document technique DT4
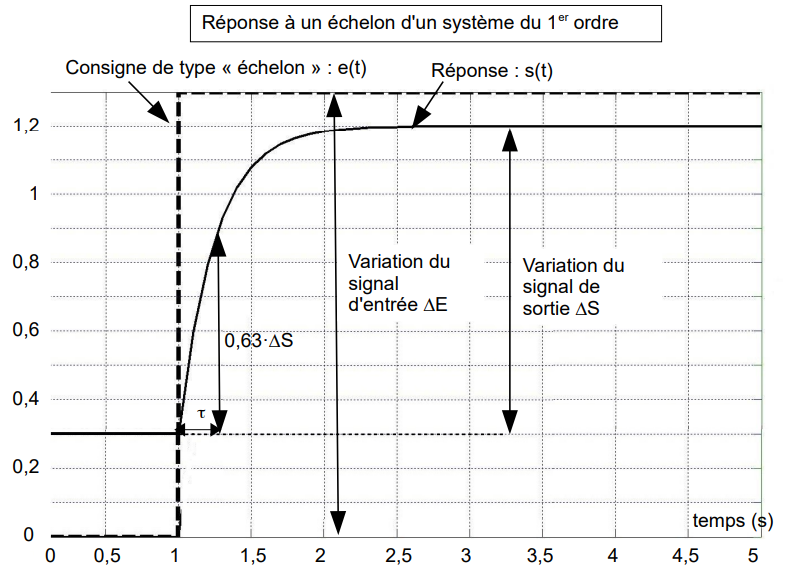
- K est l’amplification statique : \(K= \frac{\Delta S}{\Delta E}\)
- τ représente la constante de temps : durée mise par s(t) pour atteindre 63 % de sa variation ΔS
Document technique DT5
DOCUMENTS REPONSES
Document réponse DR1
Document réponse DR2
Document réponse DR3
Document réponse DR4


