Réponses du 1er et 2ème ordre
Objectif : Distinguer une réponse du premier ou second ordre. Cela peut-être utile en vue de faire la modélisation mathématique d’un objet dans le cadre d’une simulation.
Les objets techniques (systèmes, sous-systèmes ou composants) réagissent différemment selon leurs natures et selon l’excitation à laquelle ils sont soumis.
On appelle réponse indicielle la réponse à l’échelon d’une grandeur physique appliquée en entrée d’un objet technique.
Pour illustrer cela, observons plusieurs situations
- Réponse en courant dans un circuit RL
- Réponse en tension dans un circuit RC
- Réponse en vitesse d’un masse soumise à un échelon de force
- Réponse en vitesse d’une inertie soumise à un échelon de couple
- Réponse en flux thermique d’un échelon de température
Tous ces objets techniques réagissent de manières similaires mais à la fois différentes. Pourtant peu de « choses » les différencient.
Les réponses vues précédemment peuvent être classées selon deux catégories :
- Réponse du Premier Ordre
- Réponse du Second Ordre
Un moyen Mnemotechnique pour les identifier …. observer la base de « S » du mot « Second » Ordre. La tangente à l’origine du « S » est horizontale comme toute réponse du Second ordre 😉
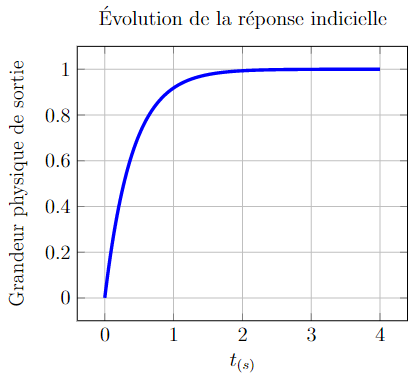
Réponses du Premier Ordre à l’échelon (réponses indicielles)
Réponses du Second Ordre à l’échelon (réponses indicielles)
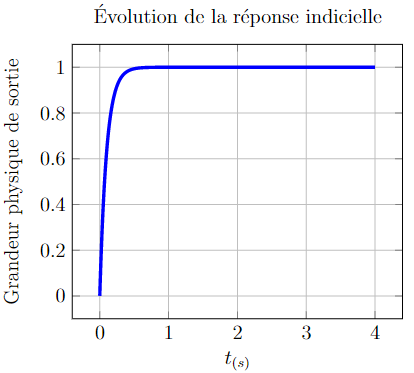
Amortissement supérieur à 1 (z>1)
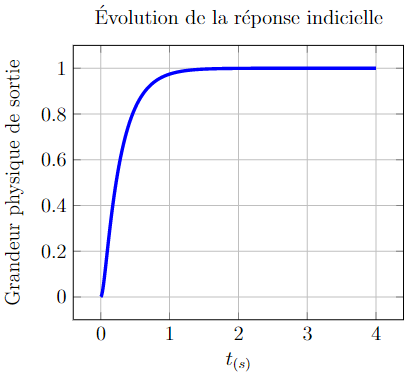
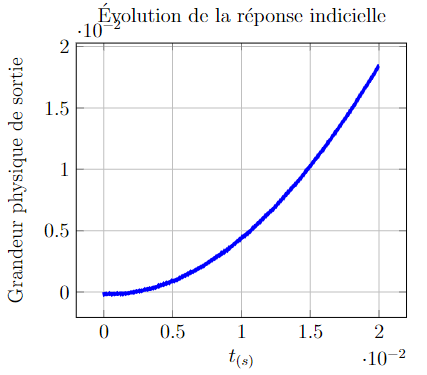
Remarque importante : on pourrait à la hâte l’identifier comme une réponse du premier ordre !! Il n’en est rien. Pour cela, rappelez vous qui faut observer la tangente à l’origine.
Observer sur la figure ci-contre l’effet de zoom sur l’origine de la courbe….
…. la tangente est nulle à l’origine, il s’agit bien d’une réponse du Second ordre ;
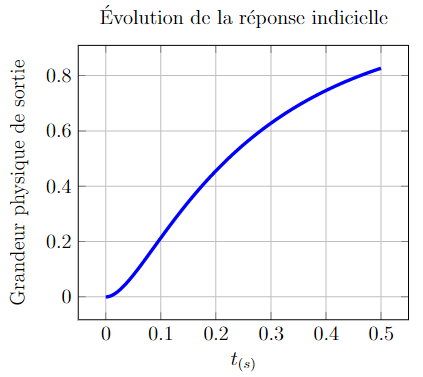
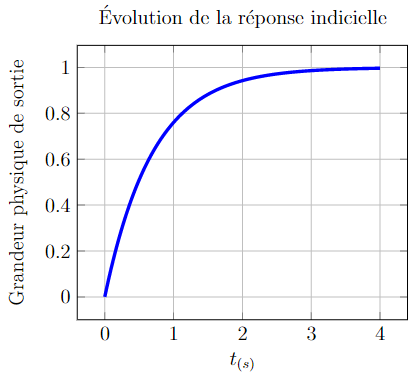
Amortissement supérieur à 1 (z<1)
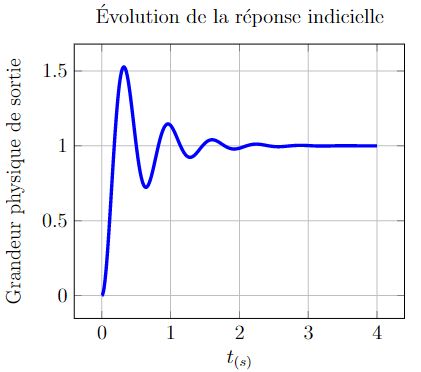
On observe un dépassement, la réponse est ainsi forcément d’une réponse à l’échelon d’un système du second ordre.
Observons tout de même la tangente à l’origine en y faisant un zoom (figure ci-contre)
La tangente nulle à l’origine confirme l’ordre 2 (second ordre) de la réponse.