Produit scalaire
Le produit Scalaire est un outil mathématique fort utile en Sciences à plusieurs titres
- projection d’un vecteur sur une base
- calcul de la puissance mécanique \(P = \vec F \cdot \vec v\) avec P en (W) F en (N) et v en (m.s-1)
- calcul de l’énergie de transfert \(W = \vec F \cdot \overrightarrow {AB}\) avec W en (J) F en (N) et AB en (m)
Il s’agit d’une multiplication entre deux vecteurs.
À retenir, le résultat d’un produit scalaire est un ….SCALAIRE !
Définitions mathématiques
Il existe trois définitions mathématiques mais seulement deux nous sont utiles en Sciences.
\(\vec u \cdot \vec v = \| \vec u \| \cdot \| \vec v\| \cdot \cos (\vec u , \vec v)\)
\(\vec u \cdot \vec v = u_x \cdot v_x + u_y \cdot v_y + u_z \cdot v_z\)
Avec les vecteurs \(\vec u\) et \(\vec u\) ayant pour composantes \(\vec u \begin{pmatrix} u_x \\ u_y \\ u_z\end{pmatrix}\) et \(\vec v \begin{pmatrix} v_x \\ v_y \\v_z \end{pmatrix}\)
À retenir : La première relation montre que le produit scalaire de deux vecteurs perpendiculaire (angle de 90° entre eux) est nul. Effectivement car le cos(90°)=0.
Soit les forces F1 et F2 s’exerçant sur la boite bleue :
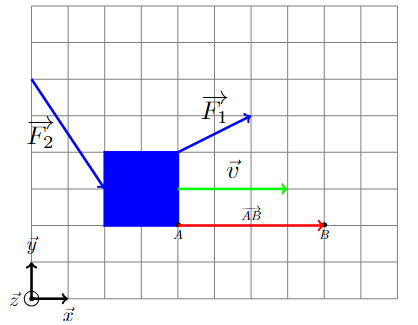
Le but ici sera de déterminer les travaux des forces F1 et F2 (Énergie de transfert) ainsi que les puissances transmises par les forces F1 et F2.
Commençons par déterminer les composantes de tous les vecteurs (\( \overrightarrow {F_1}\), \( \overrightarrow {F_2}\), \( \overrightarrow {AB}\), \( \overrightarrow v\))
Échelle :
Pour les forces : 1 carreau = 10 N
Pour les distances : 1 carreau = 1 m
Pour les vitesses : 1 carreau = 2 m.s-1
\(\overrightarrow {F_1} \begin {pmatrix} 20 \\ 10 \\ 0 \end{pmatrix}\) ; \(\overrightarrow {F_2} \begin {pmatrix} 20 \\ -30 \\ 0 \end{pmatrix}\) ; \(\overrightarrow {AB} \begin {pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}\); \(\overrightarrow {v} \begin {pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}\)
Calculons W1 et W2 (les travaux de force respectivement de F1 et F2 le long du chemin AB)
Rappel : \(W = \vec F \cdot \overrightarrow {AB}\)
Pour W1 : \(W_1 = \overrightarrow {F_1} \cdot \overrightarrow {AB}=\begin {pmatrix} 20 \\ 10 \\ 0 \end{pmatrix} \cdot \begin {pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}=20 \cdot 4 + 10 \cdot 0 + 0 \cdot 0=80~Joules\)
Pour W2 : \(W_2 = \overrightarrow {F_2} \cdot \overrightarrow {AB}=\begin {pmatrix} 20 \\ -30 \\ 0 \end{pmatrix} \cdot \begin {pmatrix} 4 \\ 0 \\ 0 \end{pmatrix}=20 \cdot 4 + (-30) \cdot 0 + 0 \cdot 0=80~Joules\)
On constate que seule la composante selon \(\vec x\) (dans ce cas particulier) travaille (contribue au déplacement). C’est normal étant donné que la composante selon \(\vec y\) est perpendiculaire au déplacement \(\overrightarrow{AB}\), ce qui s’explique par le fait que le produit scalaire de deux vecteurs perpendiculaire est nul.
Calculons P1 et P2 (les puissances respectivement transmises par F1 et F2)
Rappel : \(P = \vec F \cdot \overrightarrow {v}\)
Pour P1 : \(P_1 = \overrightarrow {F_1} \cdot \overrightarrow {v}=\begin {pmatrix} 20 \\ 10 \\ 0 \end{pmatrix} \cdot \begin {pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}=20 \cdot 6 + 10 \cdot 0 + 0 \cdot 0=120~Watts\)
Pour P2 : \(P_2 = \overrightarrow {F_2} \cdot \overrightarrow {v}=\begin {pmatrix} 20 \\ -30 \\ 0 \end{pmatrix} \cdot \begin {pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}=20 \cdot 6 + (-30) \cdot 0 + 0 \cdot 0=120~Watts\)
On constate que seule la composante selon \(\vec x\) (dans ce cas particulier) travaille (contribue à transférer de la puissance). C’est normal étant donné que la composante selon \(\vec y\) est perpendiculaire à la vitesse \(\overrightarrow{v}\), ce qui s’explique par le fait que le produit scalaire de deux vecteurs perpendiculaire est nul.
Le produit scalaire en vidéo (orienté mathématiques)
