Détermination des puissances et des énergies nécessaires à faire avancer un mobile

Pré-requis :

Vecteurs et écriture en coordonnées cartésiennes.
produit scalaire
Utilisation de OpenModelica

L’idée est d’être capable à terme de déterminer les énergies nécessaires à l’avancement d’un mobile, une voiture dans notre cas. Nous utiliserons pour cela un logiciel de modélisation multiphysique (OpenModelica dans notre cas) qui nous permettra de les déterminer dans des situations bien trop complexes pour le faire de manière analytique. Vous devrez cependant être capable de le faire sur des cas simples.

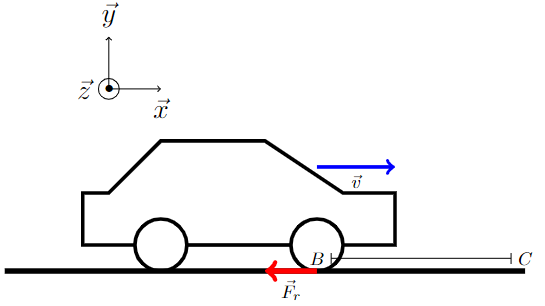
Soit une voiture (figure 1) de masse m₁=1,2 tonne se déplace sur un plan horizontal selon la loi de vitesse figure 2.

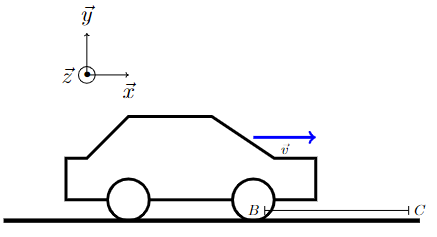
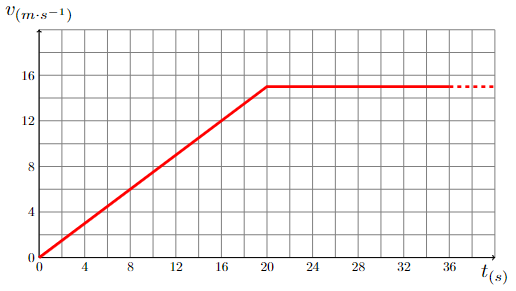
Faire apparaitre distinctement sur la figure 2 la phase d’accélération (régime transitoire) et à vitesse constante (régime établi ou permanent).
Calculer l’énergie cinétique E_c1 accumulée dans la masse de la voiture en fin d’accélération(en kJ)
Déterminer l’accélération du véhicule entre l’instant 0 s et 20 s
Déterminer la distance d₃₆ = BC parcourue par le véhicule jusqu’à la seconde 36 ainsi que la distance parcourue d_20-36 entre l’instant 20 s et 36 s.

Pour les deux phases (régime transitoire et régime établi), exprimer dans le repère (x, y et z) les vecteurs vitesse et accélération.

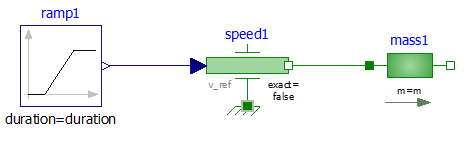
Cas le plus simple : Voiture en translation sans frottement

Il s’agit ici du cas le plus simple, absence de résistance au roulement, absence de traînée aérodynamique.

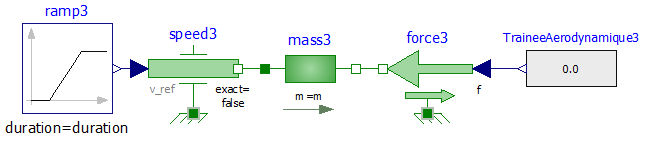
Modèle 1 *(clic droit puis enregistrer le lien sous…)*

Après avoir paramétré le modèle multiphysique (loi de vitesse et masse du véhicule), Vérifier par la simulation votre résultat à partir du modèle multiphysique.
Aide : Pour ce faire vous devez implémenter dans un bloc « RealExpression » la formule de l’énergie cinétique.

Déterminer à partir du modèle la puissance transmise et l’énergie transmise W₁ à la masse du véhicule par la force motrice.
Aide : Pour ce faire vous devez instrumenter le modèle pour déterminer les grandeurs effort et flux afin d’obtenir la puissance. Il faut pour cela ajouter des capteurs (Sensors disponible dans la bibliothèque « Mechanics/Translational »). Une intégrale mathématique (Integrator dans le logiciel) vous permettra d’obtenir l’aire sous-tendue à la courbe de puissance, donc à l’énergie de transfert transmise à la masse du véhicule

Comparer le travail de la force motrice W₁ à l’énergie cinétique E_c1 déterminée par le modèle et par le calcul.
Conclure quant à l’énergie transmise (où est passée cette énergie transmise ?)

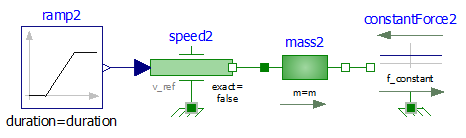
Voiture en translation avec résistance au roulement

Nous ajoutons à présent au modèle une résistance au roulement de Fr=500 N modélisée par le bloc « constantForce2 ». Le modèle suit toujours la même loi de vitesse donnée figure 2.

Modèle 2 *(clic droit puis enregistrer le lien sous…)*

Indiquer, sans utiliser le modèle, si l’énergie cinétique stockée dans le véhicule est différente à présent en raison de la présence de la résistance au roulement.

Exprimer \(\overrightarrow {F_r}\) et \(\overrightarrow {BC}\) dans le repère (x, y et z)

Calculer la puissance P_Fr de la force résistante \(\overrightarrow {F_r}\). Indiquer pourquoi cette puissance est négative.

Déterminer le travail de la force de la résistance au roulement de l’instant 0 à l’instant 36 s. Indiquer la raison de la présence du signe négatif sur le résultat.

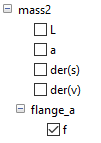
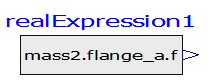
Réinstrumenter le modèle comme précédemment pour obtenir la puissance ainsi que l’énergie de transfert transmise au véhicule par la force motrice. Pour alléger le modèle on peut utiliser les blocs « RealExpression » où vous pouvez directement récupérer les grandeurs efforts et flux. Exemple : mass2.flange_a.f pour la force appliquée à mass2 coté gauche

Après avoir paramétré le modèle multiphysique, comparer la quantité d’énergie cinétique E_c2 stockée dans la masse du véhicule et le travail de la force motrice W₂. Expliquer cette différence ?

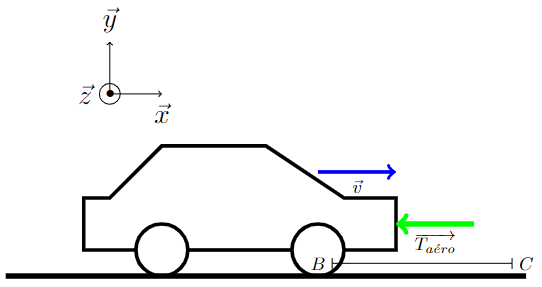
Voiture en translation avec traînée aérodynamique

Nous ajoutons au modèle de la figure 1, la traînée aérodynamique. La force de résistance au roulement est retirée pour l’exercice même si dans la « vraie vie » elle excite simultanément. Le modèle suit toujours la même loi de vitesse donnée figure 2.

Les données sont les suivantes : produit S.Cx = 0.7, masse volumique de l’air 1.2 kg.m^-3

Modèle 3 *(clic droit puis enregistrer le lien sous…)*

Indiquer, sans utiliser le modèle, si l’énergie cinétique E_c3 stockée dans le véhicule est différente à présent en raison de la présence de la traînée aérodynamique.

Exprimer \(\overrightarrow {T_aero}\)dans le repère (x, y et z)

Exprimer la puissance P_Taéro de la traînée aérodynamique \(\overrightarrow {T_aéro}\) pour les deux régimes (transitoire et établi) et calculer celle-ci à t=20 s et à la vitesse maximale atteinte, respectivement pour les deux expressions trouvées. Indiquer la raison de la présence du signe négatif sur le résultat de la puissance.

Vous remarquez que la puissance n’est pas constante ni même linéaire. Sachant que le travail de la Force aérodynamique correspond à l’aire sous-tendue de la puissance, il n’est pas aisée d’obtenir analytiquement (sauf par l’utilisation d’intégrale mathématique) cette énergie de transfert. Nous n’allons donc pas chercher à calculer analytiquement cette énergie mais plutôt utiliser la modélisation multiphysique.

Réinstrumenter le modèle comme précédemment pour obtenir la puissance ainsi que l’énergie de transfert transmise au véhicule par la force motrice.

Après avoir paramétré le modèle multiphysique, comparer la quantité d’énergie cinétique E_c3 stockée dans la masse du véhicule et le travail de la force motrice W₃. Expliquer cette différence ?

Instrumenter le modèle pour obtenir le travail de la traînée aérodynamique.
Expliquer pourquoi ce travail est négatif

Voiture en translation avec résistance au roulement + traînée aérodynamique

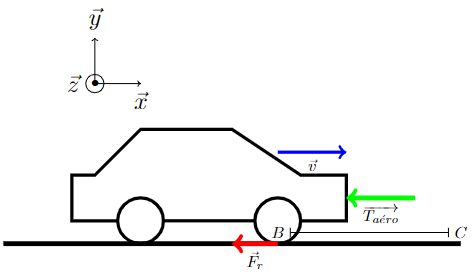
Selon le temps, réaliser la modélisation du déplacement du véhicule avec la résistance au roulement + la traînée aérodynamique.