Poussée d’Archimède
Définition
\(\overrightarrow{\prod}=\overrightarrow{Pa}=- \rho_{f} \cdot \vec g \cdot V_f\)
La poussée d’Archimède se modélise par un vecteur orienté vers le haut et appliqué en Cp (Centre de poussée). Elle représente la force exercée par un fluide sur un objet.
Avec :
\(\rho_{f}\) : masse volumique du fluide déplacé (\(kg \cdot m^{-3}\)).
\(g=9,81 m \cdot s^{-2}\) (champ de pesanteur)
Vf : Volume de fluide déplacé (m³).
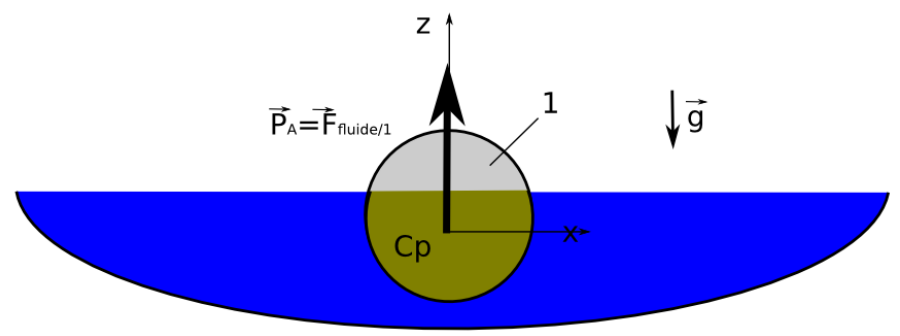
Remarque 1 : le centre de poussée Cp correspond au centre de gravité de la masse de fluide déplacé (parfois noté Gf)
Remarque 2 : tout objet dans l’air de la vie quotidienne est soumis à la poussée d’Archimède mais celle-ci est négligeable en raison de la faible masse volumique de l’air ( \(\rho_{air}=1,2 kg⋅m^{-3}\) à 15°C au niveau de la mer)
Remarque 3 : remarquer la puissance des équations vectorielles riches de sens… Sachant que Le champ de pesanteur g est représenté par un vecteur \(\vec g\) dirigé vers le centre de la terre. Il en résulte de l’équation vectorielle précédente que la poussée d’Archimède \(\vec {Pa}\) est toujours orientée vers le haut.
Quelques vidéos intéressantes…

